LIS 길이 구하기

LIS : Longest Increasing Subsequence, 최대 증가 부분수열

1. 완전탐색

int LIS(vector<int> arr) {
    if (arr.empty()) return 0;
    
    int ret = 1;
    for (int i = 0; i < arr.size(); i++) {
    	vector<int> next;
        for (int j = i + 1; j < arr.size(); j++) {
            if (arr[i] < arr[j]) {
            	next.push_back(arr[j]);
            }
        }
        ret = max(ret, 1 + LIS(next));
    }
    return ret;
}

 

시간복잡도 O(2^N)

2. DP

int cache[MAX];

int find(int start, vector<int> arr) {
    if (cache[start] != -1) {
    	return cache[start];
    }
    
    int ret = 1;
    for (int i = start + 1; i < arr.size(); i++) {
        if (arr[start] < arr[i]) {
            ret = max(ret, find(i + 1));
        }
    }
    cache[start] = ret;
    return ret;
}

int LIS(vector<int> arr) {
    memset(cache, -1, sizeof(cache));
    return find(0, arr);
}

 

완전탐색 방식에서 LIS 함수가 재귀적으로 호출되는 것을 이용해서 캐싱을 통해 중복계산 제거하는 방식

시간복잡도 O(N^2)

3. 이진 탐색을 통한 최적화

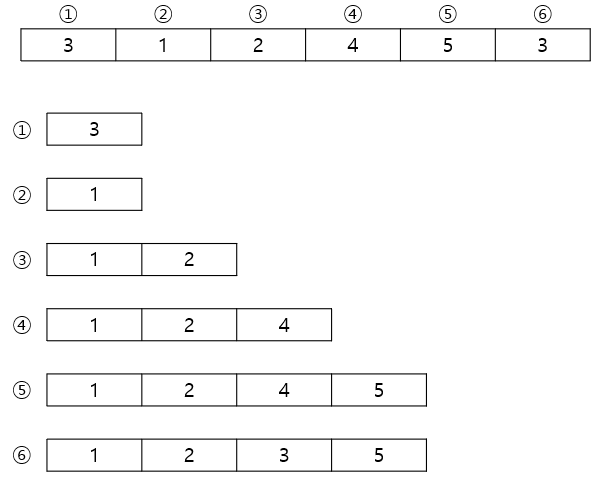
int LIS(vector<int> arr) {
    vector<int> tmp;
    tmp.push_back(arr[0]);
    
    for (int i = 1; i < arr.size(); i++) {
        if (tmp.back() < arr[i]) {
            tmp.push_back(arr[i]);
        }
        else {
            auto it = lower_bound(tmp.begin(), tmp.end(), arr[i]);
            *it = arr[i];
        }
    }
    return tmp.size();
}

 

시간복잡도 O(NlogN)

 

* 관련문제 : BOJ 11054 가장 긴 바이토닉 부분 수열